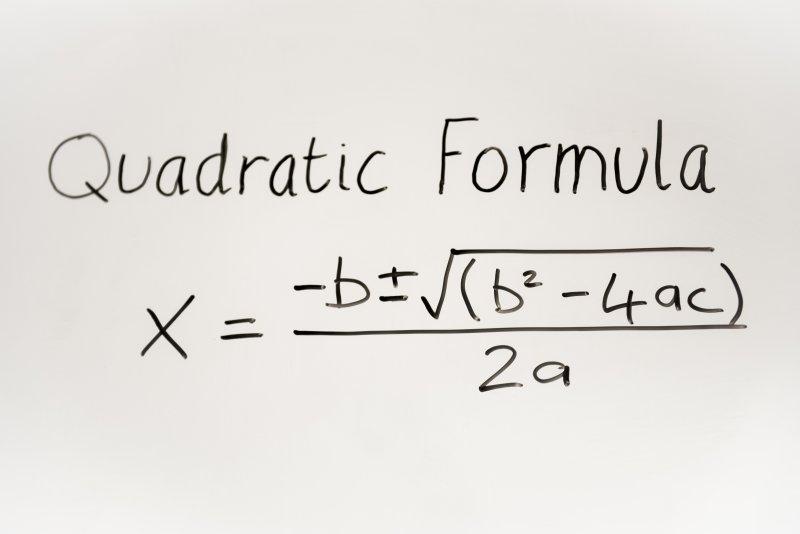So you’re studying for a test and you come across the equation x^2 + bx = c. What do you do? How do you solve it? It can seem daunting, but with a few simple steps, you can easily solve any quadratic equation.
Algebraic equations can look pretty puzzling, especially if you don’t consider yourself a math person or if it has been a long time since you worked one out for yourself. If you’re struggling with quadratic equations, or need a quick review, we put this quadratic equation solver guide together to go over the basics of solving these equations and help you memorize the formulas that you need to know.
So what is the quadratic formula – and what is the best way to solve quadratic equations? We’ll walk you through it all in this post.
What is a Quadratic Equation?
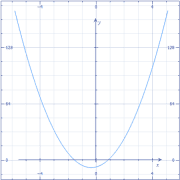A quadratic equation is a univariate equation with two solutions or roots. Wait, what does that mean? Basically, univariate means there is one variable that needs to be solved for, x. All other values in the equation are known. So if you’re only trying to solve for one value, x, why does the equation have two answers?
Quadratic equations are graphed as parabolas, symmetrically curved lines. X has two values because it represents the two places where the parabola will cross the x axis, like in the graph at the left. These graphic quadratic equations can be tricky to solve!
What Are the 5 Methods of Quadratic Equation?
There are a few methods you can use for solving a quadratic equation, including:
- Factoring
- Quadratic formula
- Completing the square
- Graphing
If you’re not sure how to use these methods, it’s best to hire a math tutor to show you the ropes. You can learn more and sign up for math tutoring here. What exactly will you learn with a math tutor? Check out this video for more information:
https://www.youtube.com/watch?v=mOeH9ZxyA8c
How to Identify Quadratic Equations
The standard form of a quadratic equation looks like this: ax2 + bx + c = 0. A, b, and c stand for actual numbers, or known values, and x stands for the unknown value, or variable. When you solve the equation, you will be determining the values for x. Here’s an example of a quadratic equation with the known values plugged in: 2x2 + 8x + 7 = 0. Note that in standard form, quadratic equations always equal zero.
Some sneaky math math teachers might present you with an equation that looks like this: x2 + 2x = 3. Don’t let this trick fool you! Simply subtract 3 from each side of the equation so that it equals zero. Remember: you have to subtract from both sides of the equation to keep it even! The result looks like this: x2 + 2x – 3 = 0.
Factoring Quadratic Equations
Some of the “easier” quadratic equations can be solved by a process called factoring. To factor a quadratic equation, take a look at the b and c values. You’ll need to find two numbers when multiplied together equal c, but when added together equal b. Don’t worry if this sounds kind of abstract. Let’s take a look at an example so you can see how factoring works.
x2 + 5x + 6 = 0
To solve this equation, you’ll need to think of two numbers that add up to five and multiply to make six. You can add two and three to make five, or multiply two times three to get six, so these are your factors for this example. You’ll want to write your answer like this: x2 + 5x + 6 = (x + 3)(x + 2). You can check your work by multiplying the factors (x + 3) and (x + 2) to make sure they equal the original equation.
Factoring an equation with negative numbers involved can be a little trickier. If c is positive, then the factors are either both positive or both negative. If b is negative and c is positive, both factors are negative. If b is positive and c is positive, both factors are positive.
If you’re looking at an equation and c is negative, this means that one factor is negative and one factor is positive. If b is positive, the larger factor is positive. If b is negative, the larger factor is negative.
Using the Quadratic Formula
Next up, is the quadratic equation formula. How to solve quadratic equations when they can’t be easily solved.
Sometimes, because life isn’t fair, quadratic equations can’t be solved with simple factoring. When you come across one of these weird and wily equations, you’ll need to bust out the quadratic formula to get the job done. The quadratic formula looks like this:
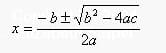
| Note that before the square root sign, there is a plus sign and a minus sign. This stands for plus or minus, which means the formula must be solved twice, once adding the root to -b and once subtracting in order to get both values for x. |
To get started, plug the values in for a, b, and c. Once you have your numbers plugged in, solve for x following the order of operations: parentheses, exponents, multiply, divide, add, subtract. A common mnemonic phrase to help you memorize the order of operations is “please excuse my dear aunt Sally”; the first letter of each word in this phrase is the same as the order of operations.
For example, solving the equation x2 + 3x – 4 = 0 would look like this:
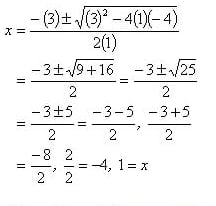
Since this equation can be factored (x + 4, x = -4, and x – 1, x = 1), you can easily check your work.
As you can see, once you have the values plugged in to the correct place in the quadratic formula, working out the answer is fairly simple. Students tend to struggle most with remembering how to construct the quadratic formula. Here are a couple of tips for memorizing this magic formula.
- Sing it to the tune of “Pop Goes the Weasel”, using these lyrics: x equals negative b
plus or minus the square root
of b squared minus 4ac
all over 2a - Memorize this story: There once was a negative boy, who was all mixed up, so he went to a radical party, but because he was square, he lost out on four awesome chicks, so he cried his way home and when the night was all over, it was 2 AM.
- Just stare at this GIF until you become one with the formula visualize the quadratic formula equation (not the best method, but it could work I guess):
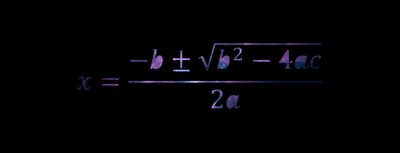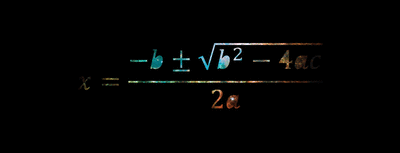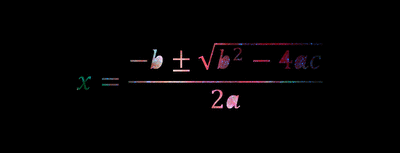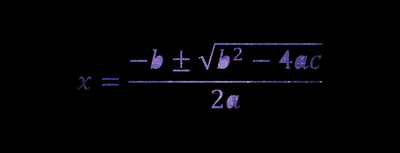
Other Important Quadratic Equation Formulas
Here are a few more formulas that might help you when questioning how to solve quadratic equations:
- For a < 0, the range of the quadratic equation ax2 + bx + c = 0 is : (∞, -(b2 – 4ac)/4a]
- For a > 0, the range of the quadratic equation ax2 + bx + c = 0 is [b2 – 4ac/4a, ∞)
- D < 0 the roots do not exist, or the roots are imaginary.
- For D = 0 the roots are real and equal.
- D > 0 the roots are real and distinct.
- For negative value of a (a < 0), the quadratic expression f(x) = ax2 + bx + c has a maximum value at x = -b/2a.
- For positive values of a (a > 0), the quadratic expression f(x) = ax2 + bx + c has a minimum value at x = -b/2a.
- The condition for the quadratic equations a1x2+b1x+c1=0, and a2x2+b2x+c2=0 having the same roots is (a1b2−a2b1)(b1c2−b2c1) = (a2c1−a1c2)2.
- The discriminant of the quadratic equation is D = b2 – 4ac
- Formula to find the roots of the quadratic equation is x = −b±√b2−4ac2a.
- The product of the Root of the quadratic equation is αβ = c/a = Constant term/ Coefficient of x2
- Quadratic equation having roots α, β, is x2 – (α + β)x + αβ = 0.
- The quadratic equation in its standard form is ax2 + bx + c = 0
- Sum of the roots of a quadratic equation is α + β = -b/a = – Coefficient of x/ Coefficient of x2.
Use a Quadratic Equation Calculator
When all else fails, you can always use a quadratic equation calculator.
Here are some links to the best quadratic equation solver calculators out there:
How to Solve Quadratic Equations?
Applying these tips should help you understand how to solve a quadratic equation. If you’re still struggling, reach out for more help. There are plenty of resources available to you and we want to make sure you get the right help so that you can succeed in your math classes. With a little effort, solving quadratic equations will be a breeze!
If you’re still having trouble working through quadratic equations, an academic tutor can give you personal attention and help you with any questions you might have. TakeLessons tutors are qualified, prescreened, and motivated to help you succeed. Tutors are available online and in-person, so search for your perfect tutor today!
You might also like…
–Test Taking Strategies: Your Guide to a Stress-Free Finals Week
–6 “Extra Credit” Results You Get With Tutoring
–A+ Tips: How to Write an Essay
–Megan L. TakeLessons Staff Member and Blogger
Photo by Ianqui
Megan L.