If the idea of sitting down to study math makes you grumble, you’re not alone. But have you ever thought about how beautiful math can actually be? Math is all around us–in nature, in architecture, and even in music–and exploring these sides of the subject can make it much more interesting! Here are a few ways that mathematics can actually be pretty amazing:
Math in Music
Rhythm, musical pitches, and more–they all have some connection to math! And as you learn to read music, you’ll notice that the theory behind it is similar to how you learned fractions. Pieces are divided into measures, measures are divided into beats, and beats can be further divided by notes of particular values. In order to play the piece correctly, you’re using your brain to figure out the math as you go along!
You can “hear” math at work in many songs that make use of complicated rhythms and syncopation, and it’s especially evident when artists superimpose two songs together (i.e. mash-ups!). These artists often use computer software and mathematical strategies to determine where certain songs will fit, based on pitch, key, harmonies, and song length.
Pythagorean Theorem Proof
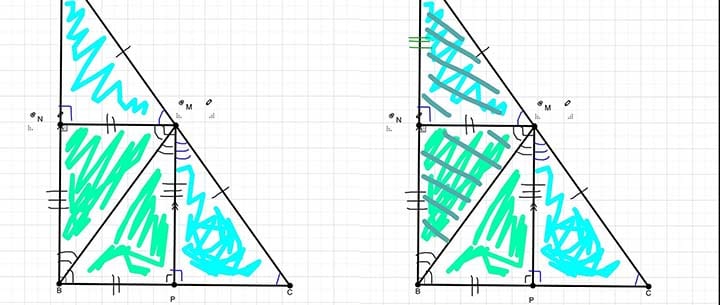
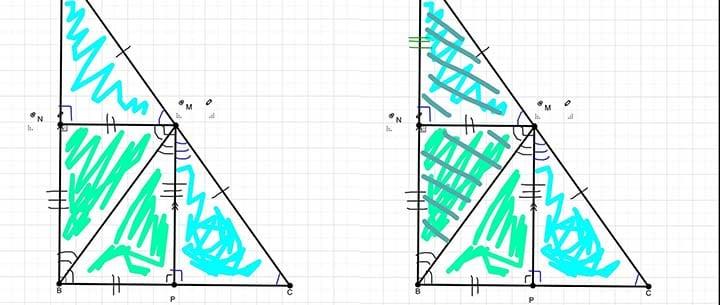
OK, this one might just be for the math nerds out there. The Pythagorean Theorem is an algebraic equation that explains the relationship between all three sides of a right triangle. It states that the sum of the squares of each side add up to equal the square of the hypotenuse.
So what makes it beautiful? When you look at a right angle triangle, it can be hard to determine the ratios at first glance. But when it’s drawn out for you (like above), not only is there a fair amount of beauty in it, but you can see how it can be rearranged and dissected. Keep this ratio in mind the next time you need to study math for a test!
Fibonacci Sequence
The Fibonacci Sequence is a set of numbers that rapidly increases, and is defined by the rule that the next number in the sequence is equal to the sum of the previous two. The first handful of numbers are: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, and so on.
If you’re working with the Fibonacci Sequence and trying to figure out how to study math while using it, consider looking into the Fibonacci Spiral (also known as the Golden Spiral). Its growth factor–the rate at which the spiral gets wider–is equal to the Golden Ratio (we’ll get into this next). For examples of the Fibonacci Spiral, think about the outward spiral of seeds on a sunflower, spiral galaxies like the Milky Way, and the mesmerizing patterns on pinecones.
Golden Ratio
As you continue further and further to the right in the Fibonacci Sequence, the ratio of a term to the one before it gets closer to the Golden Ratio, which is about 1.62. Mathematically speaking, the algebraic relationship looks like this: (a+b)/a = a/b. An easier way to think of it is to picture a rectangle, with sides a and b, where the b side is equal to a+b.
Faces that fit perfectly inside this pattern are considered handsome or pretty, and many historical buildings follows this shape as well. Other examples of where the Golden Ratio can be found include the design of the iPhone, famous paintings like Da Vinci’s “Mona Lisa”, and even the dimensions of the human body. Who knew figuring out how to study math is sometimes as simple as looking in the mirror?
Fractal Geometry
A fractal is a self-repeating pattern, at any scale in which it’s examined. A prime example of a fractal is the Mandelbrot Set, which has been heavily studied by mathematicians around the world.
Fractals defy the norms that you might be familiar with when zooming in on images. While normal images become clearer and more defined as you adjust the zoom, fractals just develop more detail. The initial image contains one large fractal sequence with smaller fractals branching off from it, and then zooming in on any particular area shows that the smaller fractals are the same as the large one, and that they too have even smaller fractal shapes branching from them.
Fractals are also evident in nature. If you’ve ever looking closely at a snowflake, you’re seeing fractal geometry at work. The snowflake begins at the macro-level with a hexagonal symmetry, and then continues with the same level of symmetry as you look closer at each individual section. This is why no two snowflakes are exactly alike–at some level each snowflake has a different type of fractal pattern.
If you’re still curious about how to study math and its hidden beauty, working with a private math tutor can be a great help. Your math tutor will cater lessons to your specific learning style, and work with you until you truly understand the material–which can be great if you are falling behind, or simply want to get ahead! Finding beauty in math doesn’t have to be difficult, and with a private math tutor you can learn how to study math as efficiently as possible. Good luck on your mathematical journey, and don’t forget to stop and smell the roses–you might notice the Fibonacci spiral in action!
Photos by rodtuk, alexanderward12, tiseb, jDevaun.Photography, SteveR
Suzy S.