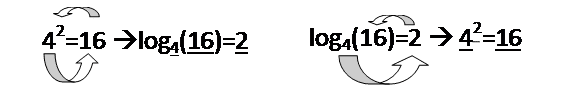Struggling with exponential and logarithmic forms? Don’t sweat! Read on as Tucson, AZ tutor Blake C. shares his strategies for solving the equations without pulling your hair out:
For many students first beginning to work with exponential and logarithmic forms, the translation between them becomes an area of confusion. The thing to remember is that, essentially, both of these forms are ways of writing the same thing.
Let’s begin our discussion by looking at the exponential form a^x=y. In this expression, some number a raised to the x power equals y. Problems involving this form may ask for any missing value, but usually this form is used when we have been given the value of a and x, and are asked to compute y.
Now, let us compare this to the logarithmic form that expresses the same relationship between a, x, and y, which is loga(y)=x. In this expression, we are being asked to determine what power of some number a would yield a resultant y. In the logarithmic form we are most often solving for the missing exponent, having been given the base a and the resultant y.
Depending on the missing value, one form or the other may be more appropriate to help us solve the equation. Typically, a missing exponent should be found using the logarithmic form and a missing resultant should be found using the exponential form. Additionally, it is often the case that we are given a form that is not best suited for finding the missing value and we will need to translate our expression from exponential form to logarithmic form, or vice versa. Thankfully, there is an easy trick for this translation process.
For the sake of this demonstration, let’s use some real values so this concept can become a little less abstract. Let us take the exponential expression 4^2=16. Now, if we are asked to translate this into logarithmic form, we can use a technique referred to as the “round-about”. See the image below to see what this technique looks like. This shows how to go from logarithmic to exponential form and how to go from exponential form to logarithmic form.
Now, let’s take a look at an example problem:
4^2=16 —> log_(_)=_
Notice we have three blanks in our logarithmic form that we have to fill. Following the round-about technique we can see that we will start with ‘4’ and move counterclockwise in a circle around our original expression to find the second value ‘16’, and finally the third value ‘2’. These values get placed into the logarithmic expression in the order we found them using our round-about, 4-16-2.
4^2=16 –>log4(16)=2
And it’s as simple as that. The round-about technique also works to go the other way, from logarithmic form to exponential form.
log4(16)=2 –> __=_
Once again we have three blanks to fill, this time though our blanks belong to the exponential form. Making the same counterclockwise motion, we start with the base of ‘4’, move to the power of ‘2’ and finish with the resultant ‘16’. These values are inserted in the exponential form in the order given by the round-about technique, 4-2-16.
log4(16)=2 –> 4^2=16
The round-about technique is a very easy way to visualize the process of moving back and forth between these forms. Drawing in the arrows can help reinforce this concept, so you can not only check to see if your answer makes sense, but also whether or not your arrows form a circle.
If you’re not a visual learner there is also a simple leapfrog concept that we can verbalize. So we simply, fill the first blank with the first number, leapfrog the middle to fill the second blank, and return to the middle to fill the third blank.
Use whichever way of looking at this process makes better sense to you and seems the easiest way to remember. And don’t forget, if you ever get stuck, a math tutor is always ready to help!
Blake C. tutors in various subjects, including math, reading, and SAT prep, in Tucson, AZ and online. A Flinn Scholar, Blake C. graduated from The University of Arizona with a degree in Business Management in 2007 and later returned for a second Bachelor’s in Music Theory History and Criticism which was awarded in December of 2013. Learn more about Blake here!
Photo by Sean
Suzy S.